Planimetria - okrąg vladimirovna: Dany jest punkt A=(−1,2) b) znajdź równanie takiej prostej przechodzącej przez punkt A, że odległość o początku układu współrzędnych od tej prostej jest równa 1 Jedną prostą znalazłam. /narysowałam dokaldny rysunek w układzie współrzędnych, z którego wynika, że druga prosta jest rowna x=2 nie wiem jak do tego dojść czy mogę to zapisac w nastepujący sposób: d(D, l_y)=1; d(A,l_y)=1; k||l_y ⇒ k→x=1 D(−1,0), A jw,, k − prosta AD ?

AS: Odległość punktu P(xo,yo) od prostej danej równaniem A*x + B*y + C = 0 wyraża się wzorem

	|A*xo + B*yo + C|
d =
	√A2 + B2

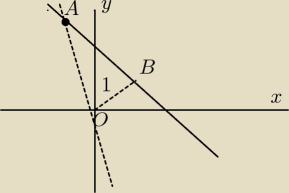
Dane: A(−1,2) , O(0,0) , OB = 1 , Szukane: y = a*x + b lub a*x − y + b = 0 Punkt A należy do prostej,wsp.tego punktu muszą spełniać równanie prostej a*(−1) − 2 + b = 0 ⇒ b = a + 2 równanie pierwsze Z wzoru na odległość punktu od prostej mamy

	|a*0 − 1*0 + b|
1 =
	√a2 + (−1)2

	|b|
1 =		⇒ |b| = √a2 + 1 ⇒ b = ±√a2 + 1
	√a2 + 1

Podnosząc do kwadratu mamy b² = a² + 1 Podstawiając b z równania pierwszego mamy (a + 2)² = a² + 1 Po rozwiązaniu otrzymujemy a1 = −3/4 , b1 = 5/4 lub a2 = −3/4 , b = −5/4 Szukane równanie

	3		5
y = −		x ±
	4		4

Uwaga: Ta druga prosta powinna niżej przebiegać

vladimirovna: no dobra ta jedną prostą mam, do tego wyniku doszłam, Tyle, że druga powinna być równa x=2 i chodzi mi w sumie o to, czy mogę to zapisać jw. podałam. Czy tamt wyrażenie dowodzi tego, ze ta druga prosta to x=2, czy trzeba do tego podejść w jakis inny konkretny sposób

Jack: na podstawie rys. nie powinnaś "dowodzić". zdecydowanie powinnaś obrać inną drogę.

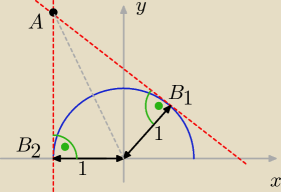
Jack: Możemy też tak zrobić: 1. Zbiór punktów odległych o 1 od początku u. współ. wyznacza równanie okręgu: x²+y²=1. Widać, że interesować nas będzie tylko górny półokrąg (można oczywiście wykonać analogiczne rachunki dla dolnego pólokręgu i przekonać się, że nie będzie rozwiązań). Zatem szukany na okręgu punkt B ma współrzędne x, √1−x². 2. Łatwo policzyć, że odległość A od B jest równa 2 (ponieważ odl. A od początku ukł. współ. jest równa √5, a promień okręgu 1). 3. Układamy równanie na odległość A(−1,2) od B(x,√1−x²), która jest równa 2. (x+1)²+(√1−x²−2)²=2² x²+2x+1+1−x²−4√1−x²+4=4 2x+2−4√1−x²=0 x+1=2√1−x² /² (zał. x+1≥0) x²+2x+1=4−4x² 5x²+2x−3=0 x₁=−1, x₂=0,6 ∊D 4. Dla x₁=−1 dostajemy, że y₁=0. Czyli punkt B(−1,0), wobec A(−1,2) oznacza to prostą x=−1 Dla x₂=0,6 dostajemy, że y₁=0,8, stąd B(0,6; 0,8) a prosta po wyliczeniu wychodzi:

	3		5
y=−		x+
	4		4

Jack: w rozwiązaniu Asa jest luka, gdy uznaje, że b może być ujemne. Nie może, ponieważ

	|b|
skoro 1=		, to widać, że b>0 (bo pierwiastek dodatni, 1 dodatnia), a nawet mamy,
	√a2+1

że b=√a²+1. A poza tym na oko widać, że nie mogą być dwie proste równoległe jednocześnie przechodzące przez ten sam punkt A... No i szukając funkcji liniowej (ax+by+c=0), odrzucił możliwość znalezienia prostej która nie jest funkcją (pionowej linii).

vladimirovna: Dziękuje Jacku! Właśnie o to mi chodziło. Bo wiem, że nigdy nie można założyć, że prosta przyjmuje wyłącznie postać kanoniczną, tyle, że bawienie sie wzorami ogólnymi jest o wiele trudniejsze, a Ty znalazłeś świetne rozwiązanie.Dziękuję Ci bardzo!

vladimirovna: Tylko jeszcze gdyby ktos mógł mi powiedzieć o tym założeniu x+1≥0. Tylko przy tym założeniu można podnieść do kwadratu, zgadzam sie. Ale nie wiem skąd się wzięło samo założenie.

AS: Ze skruchą przyznaję się do błędu,rozwiązaniem poprawnym jest tylko równanie

	3		5
y = −		x +		, drugie równanie jest prostą równoległą oddaloną o 1 od
	4		4

prostej,ale nie przechodzącą przez punkt A. Natomiast drugim równaniem,opartym na spostrzeżeniu wzrokowym jest prosta o równaniu x = −1

Jack: zgadzasz się, że tylko przy tym założeniu można podnieść do kwadratu a nie wiesz skąd ono jest? Ponieważ prawa strona jest nieujemna, to i lewa też musi być nieujemna (gdyby nie to założenie mogłoby się okazać, że dostaniemy dodatkowe, niepotrzebne rozwiązania)